martes, 22 de noviembre de 2016
Función lineal: definición
La función lineal (o función afín) de la forma f(x)=mx+b es una función polinómica de primer grado, siendo m y b números Reales. La gráfica es una línea recta y sus parámetros son:
- m: es la pendiente e indica la inclinación de la recta. Es el cociente entre la variación de la variable dependiente y la variación de la variable dependiente:
- b: es la ordenada al origen e indica el valor en donde la gráfica corta al eje de las ordenadas (eje y).
f(0)=b
EJEMPLO 1: En la función f(x)= 2/5 x+1 la ordenada al origen es -1 y la pendiente 2/5 (donde su variación en x es 5 unidades y su variación en y es 2 unidades).
EJEMPLO 2: En la función g(x)= 4-1/2 x, la ordenada al origen es 4 y la pendiente es -1/2 (por lo que su variación en x es 2 unidades y su variación en y es -1).
EJEMPLO 3: En la función h(x)= 3x, la ordenada al origen es 0 y la pendiente es 3, que escrito en forma de fracción es igual a 3/1 (así su variación en x es 1 unidad y su variación en y es 3 unidades)

ACTIVIDAD PARA RESOLVER:
Dadas las siguientes funciones determinar la pendiente y la ordenada al origen:- f(x)= 4x-9
- g(x)= 2/7 x +1
- h(x)= 5-2x
- i(x)= 5
- j(x)= -6x
- k(x)= -6-1/2 x
- l(x)= 1/2 + 3/4 x
- m(x)= x+2
- n(x)= -x-4
- p(x)= 2/3x
Ángulo de inclinación de la recta y Variación uniforme
PENDIENTE Y ÁNGULO DE INCLINACIÓN DE LA RECTA
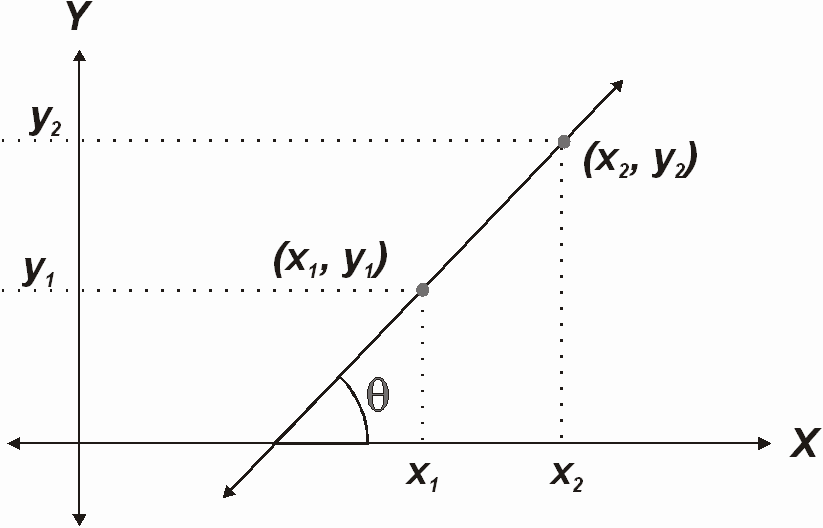
El ángulo de inclinación es el que forma
la recta con el eje de las abscisas (eje x). A partir de él también se puede
conocer el valor de la pendiente, ya que se forma un triángulo rectángulo cuyos
catetos son: la variación en x y la variación en y .
Como la fórmula trigonométrica que relaciona los catetos es la de la tangente
del ángulo podemos escribir la pendiente de la recta como:
(Para ampliar la información visita éste enlace)
VARIACIÓN UNIFORME
Una de las características de la función
lineal es la de poseer una “variación
uniforme”, es decir, que cada vez que la variable independiente aumenta o
disminuye un determinado valor, la variable dependiente también aumenta o
disminuye una cierta cantidad. Esta variación es siempre constante e igual a la
pendiente.
(Ver aquí un ejemplo)
(Ver aquí un ejemplo)
Función creciente, decreciente y constante
El valor de la pendiente determina si una
función lineal es creciente, decreciente o constante.
- FUNCIÓN CRECIENTE: Su pendiente es positiva (m>0) y el ángulo de inclinación es agudo.
- FUNCIÓN DECRECIENTE: Su pendiente es negativa (m<0) y el ángulo de inclinación es obtuso.
Ejemplo: f(x)
= 5-4x
- FUNCIÓN CONSTANTE: Su pendiente es igual a cero (m=0), por lo tanto la recta no tiene inclinación.
ACTIVIDADES PARA RESOLVER:
1) Dadas
las siguientes funciones lineales indicar si son crecientes, decrecientes o
constantes. Determinar la pendiente y la ordenada al origen, luego graficarlas (para ello puedes utilizar el graficador que se encuentra a la derecha del blog colocando la función y presionando "submit") :
a) f(x)= 3x-8
b) g(x)= -5x-7
c) h(x)= 2-1/2 x
d) i(x)= -3-4x
e) j(x)= 5-3/5 x
f) k(x)= ¾ x +1
a) f(x)= 3x-8
b) g(x)= -5x-7
c) h(x)= 2-1/2 x
d) i(x)= -3-4x
e) j(x)= 5-3/5 x
f) k(x)= ¾ x +1
2) Observar
las imágenes y determinar si la función de cada recta es creciente, decreciente o constante:
Representaciones de la función lineal
Una función puede representarse mediante su ecuación (o fórmula), una tabla de valores y una gráfica (en éste caso es una línea recta).
- ECUACIÓN: La ecuación de la recta puede presentarse en diferentes formas, la que venimos trabajando aquí es su “forma explícita”. Ejemplo: y=2x-4
- TABLA DE VALORES: Consiste en dar valores a la variable independiente y calcular los valores de la variable dependiente a partir de la fórmula. La tabla del ejemplo anterior es:
x
|
y=2x-4
|
3
|
2.(3)-4= 2
|
2
|
2.(2)-4= 0
|
1
|
2.(1)-4= -2
|
0
|
2.(0)-4= -4
|
-1
|
2.(-1)-4= -6
|
- GRÁFICA: La gráfica puede obtenerse a través de dos procedimientos:
· - Ubicando
en el plano cartesiano los puntos hallados en la tabla de valores. Para saber cómo hacerlo puedes mirar el siguiente video:
· - A partir de los valores de la pendiente y
la ordenada al origen en la ecuación. Observa la explicación del video:
https://1drv.ms/p/s!AitRk72dPr3xd86gim7bfGR-a0g
ACTIVIDAD PARA RESOLVER
e En el siguiente enlace podrás realizar una actividad interactiva en la que aplicarás los contenidos vistos hasta aquí. Para ello primero necesitas descargar el documento.https://1drv.ms/p/s!AitRk72dPr3xd86gim7bfGR-a0g
Ecuación de la recta
ECUACIÓN DE LA RECTA CONOCIENDO LA PENDIENTE Y UN PUNTO
La ecuación de la recta que tiene pendiente m y pasa por el punto (x1;
y1) es:
y-y1= m.(x-x1)
Se denomina "forma punto-pendiente" de la ecuación de la recta.
Ejemplo: si la recta tiene pendiente -3 y pasa por el punto (1; 3), entonces sustituyo en la forma punto-pendiente los valores de m= -3, x1 =1 y y1 = 3:
y-3= -3.(x-1) despejo y
y-3= -3x+3 aplico por propiedad distributiva
y= -3x+3+3
y= -3x+6 Ecuación de la recta
Si no te ha quedado claro puedes ver el siguiente video:
ECUACIÓN DE LA RECTA CONOCIENDO DOS PUNTOS
Ejemplo:
para hallar la ecuación de la recta que pasa por los puntos P1=(3; -9) y P2=(-1; 11), primero se
calcula la pendiente con la fórmula:
Luego se utiliza la forma punto-pendiente de la ecuación para sustituir allí el valor de la pendiente calculada y los valores x1 e y1 por las coordenadas de cualquiera de los dos puntos dados. Por último se despeja y:
y-y1= m.(x-x1)
y-(-9)= -5.(x-3) sustituyo los valores (tomé el punto (3; -9) )
y+9 = -5x+15 aplico por propiedad distributiva
y = -5x+15-9
y = -5x+6 Ecuación de la recta

En el siguiente video puedes ver otra forma de hallar la ecuación de la recta que pasa por dos puntos:
ACTIVIDADES PARA RESOLVER:
1) Hallar
las ecuaciones de cada una de las rectas que cumplen con las siguientes condiciones:
a) Contiene
al punto P=(3; 2) y tiene pendiente igual a -2.
b) Pasa
por los puntos P1=(-5; -4) y P2=(-4; -2).
c) Pasa
por el punto Q=(-1¸-9) y tiene pendiente igual a -9.
d) Contiene
a los puntos A=(2; 10) y B=(1; 3).
e) Pasa
por los puntos P=(-3; -8) y Q=(7; 2).
f) Tiene
pendiente m=1 y contiene al punto A=(7;
4).
g) Pasa
por el punto D=(-7; 2) y tiene pendiente m=3/7.
Luego grafica cada una en el graficador que se encuentra a la derecha del blog, (para ello colocas la función y presionas "submit") y verifica que tales rectas pasan por los puntos indicados.
Luego grafica cada una en el graficador que se encuentra a la derecha del blog, (para ello colocas la función y presionas "submit") y verifica que tales rectas pasan por los puntos indicados.
2) Determinar
la ecuación de la rectas que se muestran en las siguientes imágenes:

Rectas paralelas y perpendiculares
RECTAS PARALELAS: dos rectas son paralelas, si y sólo si,
sus pendientes son iguales.
Ejemplo: Las rectas de las funciones:
f(x)
= ½ x +3
g(x)
= ½ x -1
son paralelas porque la pendiente en
ambas es ½ .
RECTAS PERPENDICULARES: Dos rectas son perpendiculares, si y sólo si, sus pendientes son inversas y opuestas.
Ejemplo: Las rectas de las funciones:
f(x)=
2/3 x +1
g(x)=
-3/2 x +4
son perpendiculares porque en f(x)
la pendiente es 2/3, y en g(x)
es -3/2.
EJEMPLO: Hallar la recta paralela a y= 5/3 x -4 que pasa por el punto P1 = (-3; -4), y la recta perpendicular que pasa por el punto P2 = (10; -3).
Primero hallamos la recta paralela, la cual tendrá la misma pendiente: m1
= 5/3 , por lo que podemos comenzar a escribir su ecuación como:
y1= 5/3 x +
b
Para calcular el valor de la ordenada al origen, sustituimos los valores de x e y por los valores del punto por el cual debe pasar dicha recta: P1 = (-3; -4) y despejamos b:
-4= 5/3 .(-3) + b
-4= -5 + b
-4+5 = b
1 = b ordenada al origen de y1
De ésta manera podemos escribir la
ecuación de la recta paralela como:
y1= 5/3 x + 1
Proseguimos con la ecuación de la recta perpendicular, cuya pendiente es
inversa y opuesta a la de y= 5/3 x -4 , por lo que su
pendiente será: m2 = - 3/5 y su ecuación:
y2= - 3/5 x + b
Utilizamos la misma estrategia aplicada
anteriormente, pero con el punto P2
= (10; -3):
-3 = - 3/5 .(10) + b
-3 = -6+b
-3+6 = b
3 = b ordenada al origen de y2
Por lo tanto la ecuación de la recta perpendicular es:
y2 = - 3/5 x + 3
(También se podría haber utilizado la forma punto-pendiente para hallar la ecuación)
ACTIVIDADES PARA RESOLVER:
1) Hallar la ecuación de la recta paralela a y=3x-4 que pasa por el punto P=(-3; -10). Graficar (Para ello puedes utilizar el garficador que se encuentra a la derecha del blog, colocando la función y presionando "submit").
2) Determinar la ecuación de la recta perpendicular a y=2/3 x-1 que pasa por el punto Q=(4; -2). Graficar.
3) Teniendo en cuenta la ecuación de la recta y= 2/5x -3 hallar:
La recta paralela que pasa por A=(8; -18).
a) La recta perpendicular que contiene a B=(10; 1).
b) Una recta paralela cuya ordenada al origen sea positiva.
c) Una recta perpendicular cuya ordenada al origen se igual a 2.
d) Graficar todas las rectas en un mismo sistema de ejes cartesianos.
4) Hallar la recta que pasa por los puntos P=(2; 8) y Q=(-1; 7). Luego:
a) Determinar una recta paralela a ella que contiene al punto R=(2; 11).
b) Encontrar la recta perpendicular que pasa por S=(5; 3).
c) Graficar las tres rectas en un mismo sistema de ejes cartesianos.
Haciendo clic aquí puedes observar problemas de aplicación resueltos y otros para resolver.
Haciendo clic aquí puedes observar problemas de aplicación resueltos y otros para resolver.